Strange Dreams and Math
2007-11-02
Category: GeneralI awoke in the middle of a dream. It was a strange dream. It involved math and proving a point. The ability to do math to explain one?s self is probably good, but I?m not sure of the psychological health of a person who does it in his sleep; especially when there are softer curves to dream about.
The modification of some shelves required knowing the outside diameter of some plastic cylinders. The shelving is the type where four plastic tubes hold up about four plastic shelves. A decision was made to add cross member on the sides to keep things from falling out that way. I needed to know if the tubes would fit standard PVC plumbing fixtures.
To measure the diameter, I hooked the end of my measuring tape on the side and swung the tape across the end of the tube. I assumed the widest measurement to be the diameter. The person working with me, who did have the afore-mentioned softer curves, demanded to know how I could trust that measurement to be the right one.
That?s where the math comes in. You may have heard terms like ?limit? and ?trigonometry? in school and wondered why such things could ever be useful. You may even have been frightened off only to hide from math for the rest of your life. Well, I?m here to tell you that math is your friend. It may be your friend who drinks all your beer, runs up your phone bill, and forgets to pick you up at the airport, but it is your friend none the less. Here is why.
We want to know if the widest part across the pipe is the diameter. We can imagine the end of the pipe as a circle. The distance from the center of the circle to the starting point, where the edge of the tape is hooked, is the radius that we will call x. Remain calm.
We also remember that the distance straight across the circle, from the start point, through the center, and ending on the other side is called the diameter. The length of the diameter is the distance of the radius x twice (outside to center and then to outside again). We denote this two times x as 2x.
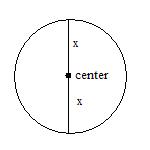
So now we have that the distance straight across is 2x, we need to determine if any other distance could be wider. That?s where the real math comes in. (In actuality, math professionals consider this stuff extremely rudimentary. They mock my limited mathematical ability. On the other hand, I?ve actually made love to women.) Figuring the other distances in general requires triangles.
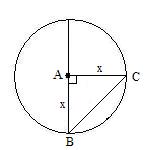
First, we make a triangle by labeling the various points. The center of the circle is labeled A. The place where the tape hooks onto the edge is called B. The other point on the edge we will call C. Keep in mind that these labels are just something I made up and they have no magical or predefined meanings. The distance between A and B, called distance AB, is the radius of the circle x. The distance AC is also the length of the radius x. What we want to know is if the distance between B and C (distance BC) is ever bigger than 2x.
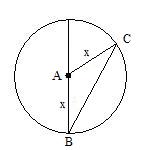
If you draw lines between A, B, and C, you form a triangle. Two sides of the triangle have the same length, namely x. That means we have an isosceles triangle. This makes it easier to figure out the distance BC.
In our triangle, the distance BC is called the ?base of the triangle?. To figure out the base of an isosceles triangle, you draw another line from point A straight down to the middle of the base, in this case line BC. We will mark that middle point as M. The new triangle AMC is a ?right triangle? meaning that it has a 90 degree angle in it. That lets us use simple formulas to calculate the distance MC and since that is half the distance of BC, it?s suddenly easy to figure BC.
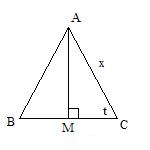
At this point, most of you are really bored with the much of the explanations, so I will get to the chase. The distance MC is x times the cosine of angle MCA in radians, labeled 't'. Radians are the units of measure best used with cosines and they really do make things easier once you get used to them. To convert your degrees to radians, multiply them times ![]() and then divide by 180.
and then divide by 180.
Since distance BC is twice the distance MC, we just multiply the whole thing times two.
distanceBC = 2xcos(t)
There a lot of places to measure as you go around a circle, and who has that much time or interest? That?s why we use a concept called a limit. Limits are a really useful mathematical concept. Limits say, ?What does it look like we will get if we start to move over there?? We have three areas where we would have concern: when the triangle ABC is almost completely wide open, when the triangle ABC is almost completely closed, and when triangle ABC is a right triangle.
When the triangle is wide open (like me, it?s called obtuse) the angle BAC is nearly 180 degrees. In radians that is 2![]() . The total degrees of all the angles of a triangle must be 180 degrees (2
. The total degrees of all the angles of a triangle must be 180 degrees (2![]() ), so the angle at point C is 2
), so the angle at point C is 2![]() minus the angle A, all divided by 2 (because B and C have to share equally). Well, if A is effectively 2
minus the angle A, all divided by 2 (because B and C have to share equally). Well, if A is effectively 2![]() , then C is zero. Using our formula from above to figure out distance BC we have 2 times x times the cosine of zero. That works out to 2x, the same as our diameter.
, then C is zero. Using our formula from above to figure out distance BC we have 2 times x times the cosine of zero. That works out to 2x, the same as our diameter.
Of course, we cannot have a triangle where one angle has the entire 180 degrees, but we can approach it. That is where the limit comes in. We ask what happens to our value as we get close to having one angle use all the 180 degrees. So, instead of letting C be zero, we let C be .0001. The cosine of zero is one, but cosine of .0001 is approximately .9999999. Now our distance BC is 2 times x times .9999999 which comes to 1.9999998x which is smaller than 2x if only a little.
Going the other way, our angle A gets close to zero degrees. That leaves 2![]() to split between angles B and C. The distance BC becomes obviously small.
to split between angles B and C. The distance BC becomes obviously small.
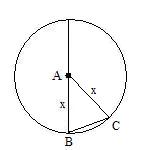
The last case is the middle of the road. This is where angle A is 90 degrees, or ![]() radians. This is a right triangle so we can use the Pythagorean Theorem. That may seem much more familiar to most of you. That?s one that says a2 + b2 = c2. The result of this gives a distance of x times the square root of 2. That is approximately 1.41x and is obviously much smaller than 2x.
radians. This is a right triangle so we can use the Pythagorean Theorem. That may seem much more familiar to most of you. That?s one that says a2 + b2 = c2. The result of this gives a distance of x times the square root of 2. That is approximately 1.41x and is obviously much smaller than 2x.
There are a few things one can learn from all of this. First, math has plenty of applications in the world. Secondly, with a little regular practice doing math is not that hard. It?s like any other skill; you just have to do it for a while. Thirdly, old LibertyBob has some mighty strange dreams and really should get out more.
Comments (5)
